The Hardy-Weinberg equation is a means by which the frequency of two alternate alleles can be predicted within a population
For two alleles of a given genetic characteristic, three genotypes are possible (assuming Mendelian inheritance): AA, Aa and aa
- Dominant allele is A, with a frequency of p
- Recessive allele is a, with a frequency of q
The Hardy-Weinberg Equation
• The total frequency of both alleles will be 100% – in other words: p + q = 1
• Because genotypes consist of two alleles, this equation must be squared: ( p + q ) 2 = 1
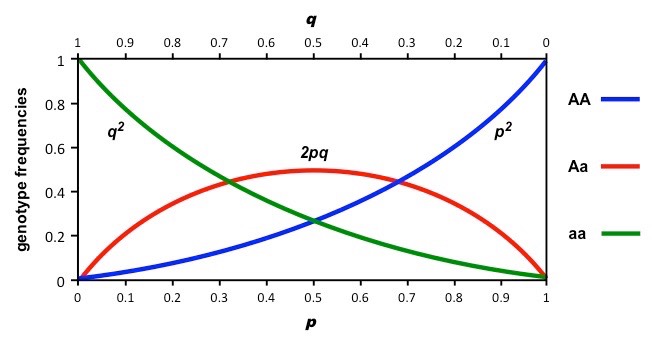
• This gives the expanded Hardy-Weinberg equation: p2 + 2pq + q2 = 1 (whereby p2 = AA ; 2pq = Aa ; q2 = aa)
Graphical Representation of the Hardy-Weinberg Principle
Hardy-Weinberg Conditions
For the Hardy-Weinberg equation to be accurate, certain population conditions are assumed:
- The population is large with random mating
- There is no mutation or gene flow
- There is no natural selection or allele-specific mortality
Worked Example
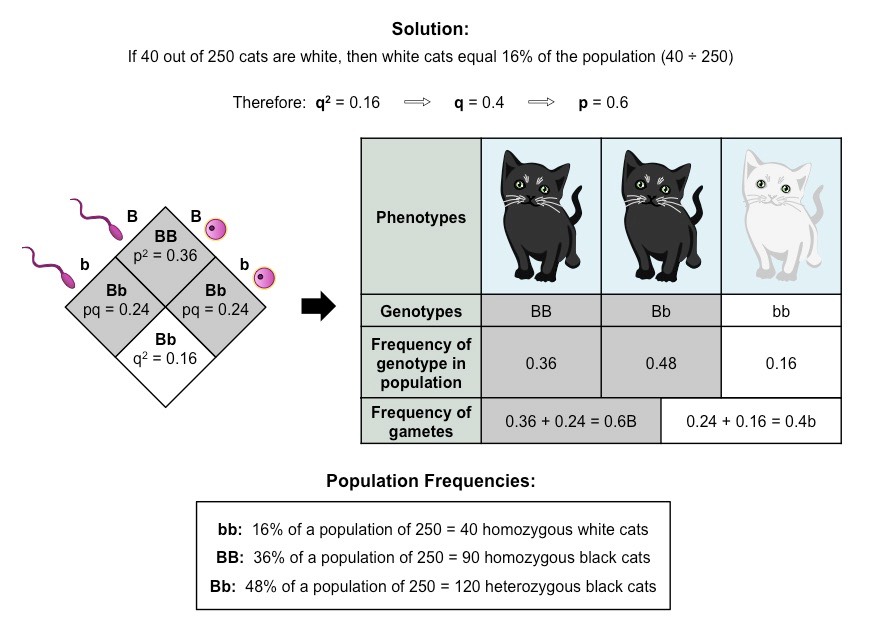
Suppose we had a population of 500 people, in which 9% were albino (albinism is a recessive characteristic)
- How many individuals in this population are heterozygous?
Using the equations: p + q = 1 and p2 + 2pq + q2 = 1
- If q2 = 0.09 ⇒ q = 0.3 (√ 0.09)
- If q = 0.3 ⇒ p = 0.7 (p + 0.3 = 1)
- If p = 0.7 ⇒ p2 = 0.49 (0.72)
- 2pq = 0.42 ⇒ (0.49 + 2pq + 0.09 = 1)
Substituting these numbers for frequencies and applying them to the original population shows that:
- 49% of people are homozygous dominant (AA), which is 245 individuals (0.49 × 500)
- 9% of people are homozygous recessive (aa), which is 45 individuals (0.09 × 500)
- 42% of people are heterozygous (Aa), which is 210 individuals (0.42 × 500)
Practice Question
In cats, the trait for black fur (B) is dominant to white fur (b).
